Is It Easy to Solve Heat Equation for Arbitrary Boundary Conditions

In this new post serial, we are going to prove you that a grand unification of gravity inside a quantum field theory framework can explicate topologically nontrivial dynamics observed in simulations of graviton inelastic collisions in a AdS space. Allow'due south get!

Information technology's all proficient. We're merely messing with your mental sanity.

Ok. At present that we have caught your attending, allow the states snap back to reality — maybe one mean solar day we will pay this topic some attending!

Even though nosotros won't achieve such an ambitious goal as the i mentioned above, in this final mail service of the Rut series, we are going to fulfill our overarching hope:

to showcase the forcefulness and versatility of Neural Networks (NNs) in solving difficult Partial Differential Equations (PDEs) in challenging domains and weather.

In this terminal instalment of the Heat series, nosotros delve once more into this topic with the aid of our very cherished Heat Equation. So let's go!

Heat #3: The Heat Equation (and a Generalized Neuro-Solver)

A very simplistic system (then far)

So far in this serial, we showcased a classical algorithm (in Estrus #1) and a Neural Network (NN) (in Estrus #ii) to solve the Heat equation. Both of these implementations were performed on an extremely simplistic (and unrealistic) scenario.
It is every bit straightforward as it tin get:

• the heat equation is a linear PDE: the solution function and all its partial derivatives occur linearly, without any cantankerous products or powers and whatsoever spacial preference for any of the (only) two coordinates. This grade of PDE is one of the simplest we can face.
• a very idealized medium with a abiding diffusivity \(D\) was used: absolutely a huge simplification, every bit it assumes a perfectly homogeneous and stationary medium. In a more plausible setting, we would have to consider a function \(D(t, x, y)\) instead.
• very simplistic conditions: the geometry considered of a square plate where the boundaries are always kept fixed and the heat flow uniformly fix along the upper boundary is quite utopian in practice. Real-life plates have deformities, changes in density, imperfections…

And so, we ought to ask the question:

How tin nosotros strengthen our example — that NNs tin can handle more complex and nontrivial cases?

This is exactly what we want to address. We will ramp up the complication of these scenarios and encounter how well NNs can potentially fare.

This won't be done with much sophistication — the approach we adopt is very incremental and straightforward. Most importantly though, it serves the purpose of a simple demonstration of the principle of generalizing learning algorithms.

Rethinking the NN architecture

Ok. What do we mean by generalization ability?

Think of a PDE — autonomously from the structure of the differential operators acting on the solution, at that place are many other variations that can touch on its beliefs: internal parameters (such as concrete properties) but besides the initial and purlieus weather (IBCs).

Getting a NN to learn for a particular instantiation of these conditions is hard on its ain. We could naively consider calculation extra dimensions and run a NN that would exist trained point past bespeak by grid-searching on yet a bigger infinite.

This surely does non sound scalable. If we want to see the consequence obtained from ever-so-slightly dissimilar conditions on the aforementioned PDE, we accept to rerun the whole classical method or perform the unabridged NN training task again.
This is highly unsatisfactory!

Worse still: the required fourth dimension to train the PINN increases rather substantially. Generalization ability requires heavy computational resources and routines that must handle the completion of the algorithm efficiently. In either case, the training fourth dimension naturally becomes a major clogging.

How to tackle these issues?

Hard-(en)coding the variability

At that place are ii direct answers — either nosotros straight:

• decrease the training fourth dimension by exploiting some magically-enhanced novel procedure which tin can accelerate the PINN's weights and biases plumbing equipment somehow. As nosotros discussed before, this seems quite unlikely and it is unclear if this cistron could annul the scaling effects.

• increase the yield from that training process: what if, for the same effort in preparation, we could obtain better predictions or encompass a larger ready of concrete cases?

It is from the second direction that the generalization idea comes out. Given that we will accept to train our PINN anyhow,

why don't we try to make it acquire the solution function for different sets of internal or external factors from the get-go?

We can do this by difficult-coding the prescription of conditions or parameters by including appropriate representations in input infinite directly in the model. Only and then we can say the model has a shot at learning for generalized cases.

Merely this isn't picayune by itself. Imagine you want to employ a vanilla NN in a supervised way. To train it, you lot would need a ground truth given by say, a classical algorithm. Each such procedure would take to rerun for each new set of parameters or atmospheric condition. This tin can accept a lot of time.

On top of that, how to know which conditions to sample from? Depending on the quality of the sampling used to generate the ground truth (in this case given past a classical simulation algorithm), the model can now in principle be used as an oracle which, if well trained, volition return confident outputs for unseen parameters. But we at present know sampling the phase space can be extremely slow or downright unfeasible in this setting. And so we may wonder:

But what if nosotros don't need a footing truth at all in our NN?

Well, we would bypass the need to run expensive and heavy classical algorithms!

Granted, constructing efficient neuro-solvers is far from picayune. However, the effect of such hard and laborious work to get the model to learn the generalized task can be huge — a considerable advantage in favor of NNs, as their inference can be significantly faster than classical methods.

If NNs succeed in this task, they can potentially solve PDEs in theoretically all possible conditions! In this perspective, NNs replace "grid-similar" algorithms where adding such parameters results in an exponential curse of dimensionality.

It sounds powerful, right?

Now, permit's become things on more concrete footing… You lot know the drill: it'south time to become hot in hither!

A neuro-solver for the Heat Equation

We have been advertising PINNs (Physics-Informed Neural Networks) for their flexibility as a DL framework, so you guessed information technology correct — nosotros are going to employ them to showcase how generalizational ability can be harvested from picking appropriate algorithms that can handle such beasts as dem' mighty PDEs!

To test these notions of generalization, we will consider our usual setup of heat diffusion beyond a 2d rectangular plate:

Fig. i: The usual initial and boundary conditions (IBCs) we assume to solve the Heat Equation on the 2D plate. Credits: David Carvalho / Inductiva

More details tin can be found in Heat #ane and Heat #ii, but let's also bear witness the Oestrus Equation in this setting for concreteness. It states that the temperature profile \(u(t,x,y)\) must satisfy:

$$ \left[ \frac{\partial}{\partial t} - D \left( \frac{\fractional^2}{\partial ten ^2} + \frac{\fractional^2}{\fractional y ^two} \right) \right]u(t,10,y)= 0, $$

With it, allow'due south investigate three topics:

• Learning for parametrized boundary atmospheric condition: keeping this admittedly unproblematic domain, nosotros parametrize the summit edge temperature \(u_{\rm top}\) into our PINN. After the network has been trained, we compare its prediction for an unseen top edge temperature by benchmarking it with respect to the classical algorithm (FDM) output.
• Learning for different domains: we see how well PINNs can solve when using more complex geometries. Nosotros will solve the Estrus Equation with a PINN in a more challenging domain, where a spherical hole is punched into the interior of the plate.
• Learning without generalizing: we will criterion how much slower it gets if generalization principles are neglected. In other words, nosotros will adress generalization past beast forcefulness. Using our new holed plate, we will run PINNs that tin can solve across this harder domain when trained (each at a time) for various diffusitivities \(D\).

Let's Heat run

You don't demand to plan anything — you lot tin can find and run our code in our dedicated github repository here and train your powerful PINNs!

Getting a PINN to generalize across purlieus conditions

Until now, but stock-still scenarios for which the purlieus and initial atmospheric condition were set a priori were used (like the ones only above). In this framework, the PINN is trained to fit exclusively with those weather.

This is naturally far from ideal. If we were to change the initial temperature of any edge by a teeny tiny bit, the model output for such a organisation would already exist of dubious predictive power!

So, we face up a structural question here:

How can we encode this boundary data as input to the PINN in a fashion the model can effectively generalize its effect on the output solution?

To answer this, let's focus on an extremely unproblematic setup to showcase this training capability. We volition keep all boundary and initial conditions stock-still except for the temperature of the top edge, which can now change.

One time once again, we choice the simplest arroyo to reach generalization: via parametrization. In this way, we think of encoding the variation past ways of variables (or any other sensible descriptor) to allow the NN to extend the solution part to other IBCs natively in its architecture.

In this elementary configuration, a single parameter \(u_{\rm top}\) volition go an boosted input.

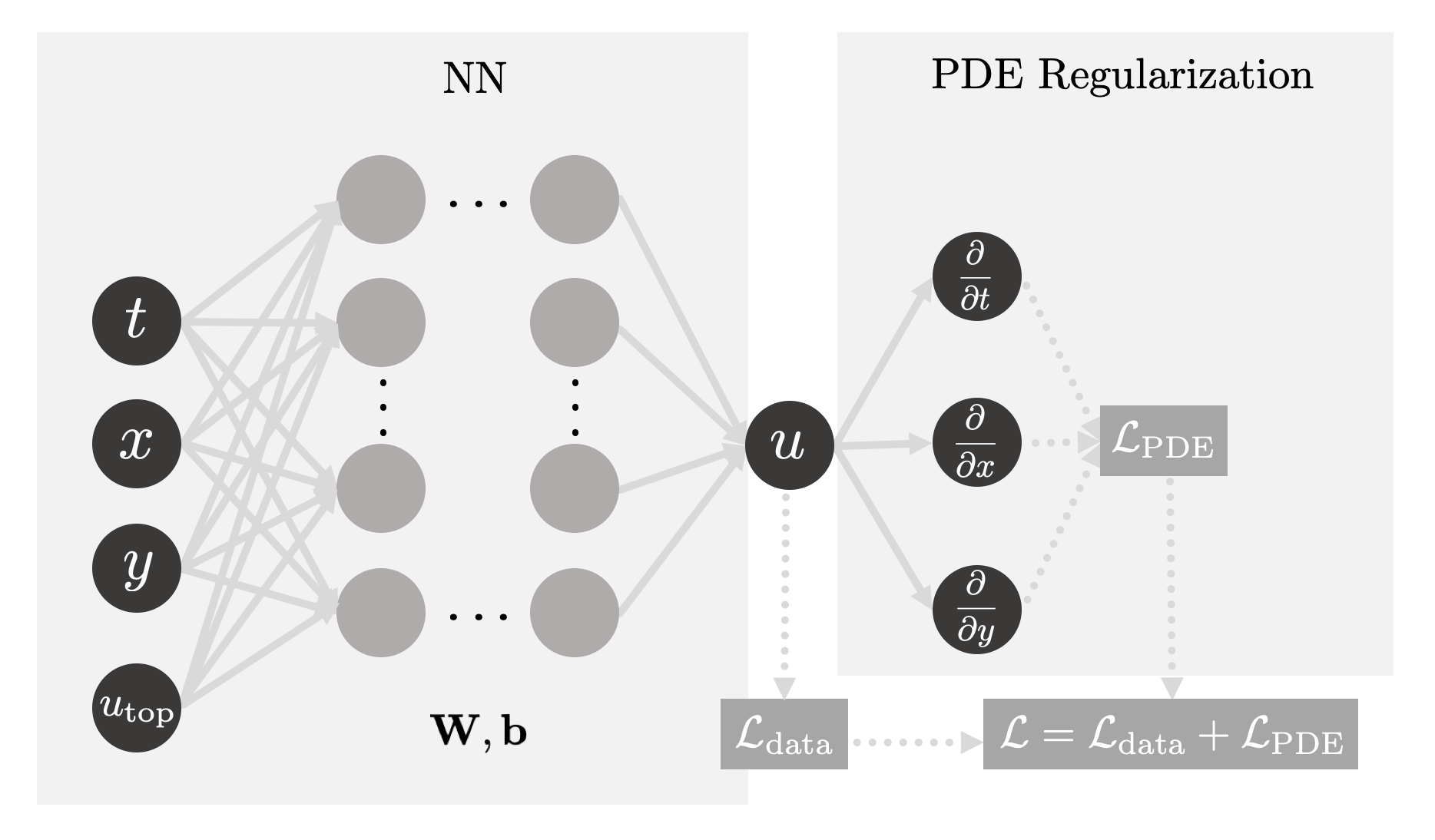
Fig 2: Our PINN will at present be able to learn the behavior of the solution equally the hot edge temperature \(u_{\rm top}\) is an input of the model. Credits: David Carvalho / Inductiva

To see how well the PINN fares, nosotros:

• train it past sampling many instances of \(u_{\rm top}\) within the range \([-i, 1]^\mathrm{o}C\).
• and so infer for the unseen case \(u_{\rm top} = 0^\mathrm{o}C\).

Running…

Exercise you remember when in Heat #2 nosotros mentioned that our implementation was able to accommodate some extra complexity? Time to exploit it!

The control line instruction to trigger this experiment and generate the PINN output is simply:

          python heat_idrlnet.py --max_iter=10000 --output_folder=generalization_bc --hot_edge_temp_range=-i,i --hot_edge_temp_to_plot=0 --output_num_x=500 --output_num_y=500 --colorbar_limits=-1.ii,1.2                  

The script heat_idrlnet.py trains a PINN in the setting described throughout the Heat series. The flags in this command line fulfill different purposes:

• max_iter defines the total number of training epochs;
• output_folder determines the directory where the resulting files stemming from the PINN preparation process are stored;
• hot_edge_temp_range is the range of hot edge temperatures within which the PINN is trained;
• hot_edge_temp_to_plot is the hot edge temperature to which we intend to infer results;
• output_num_x and output_num_y define the discretization along the ten-axis and y-axis, respectively, of the grid in which we infer results;
• colorbar_limits defines the range of the colorbar used.

Allow's analyze it past using a classical Finite Departure Method (FDM) for \(u_{\rm top} =0 \;^\mathrm{o}C\)) as the benchmark.

Fig. 3: A PINN estimate of the solution of the Oestrus Equation for a elevation edge temperature \(u_{\rm top} = 0^\mathrm{o}C\) [meridian], the output generated by a classical (FDM) method [middle] and their difference [bottom]. Credits: Manuel Madeira / Inductiva

Very overnice! As expected, the network [superlative] recovers the diffusion patterns predicted by the classical algorithm [middle]. We tin track the error by plotting their difference [bottom], where a keen resemblance arises. This plot can exist easily obtained by running the provided heat_error.py python script. Nosotros notice that the chief source of error is plant in the upper corners where cold and hot edges arrive touch, generating an extremely sharp transition that the PINN struggles to go along up with.

Even though some minor numerical deviations are seen, these are justifiable given that the task that nosotros have provided to the PINN is significantly harder, and we kept the total number of epochs and Neural Network architecture every bit before in the series.

Lesson: for the same corporeality of grooming, clever architectures can indeed provide us the generalization ability nosotros sought, saving us a huge amount of computation resources and with very trivial harm in results accuracy!

A hole lotta dearest
Probing complex geometries

We are interested in testing PINNs for more complex geometries than the regular square plate. Let united states so now become the extra mile and accost precisely the challenges of probing different domains with NNs.

PINNs are especially well suited to address complex geometries as it only requires a proper domain sampler that provides both:

• purlieus and initial points with the correct target value (given by the ground truth);
• and interior points where the PINN computes the PDE residual so backpropagates it.

In fact, the PINN solution role will be defined for values outside of the domain considered, but we just fail it.

Our lawmaking implementation supports designing a plate with an arbitrary number of holes inside the problem domain. Let's focus on a unmarried hole at the plate eye:

Fig. 4: We now generalize our boundary and initial conditions given the domain past taking the peak edge temperature every bit a variable parameter \(u_{\rm superlative} \in [-ane,1] \;^\mathrm{o}C\), while the hole purlieus is of the hot or cold type. Credits: David Carvalho / Inductiva

Given this, we keep the boundary and initial weather condition as in the previous setting (pinnacle border at the maximal temperature (\(u = 1\;^\mathrm{o}C\)) and the rest of the boundaries and initial points at the minimal temperature (\(u = -1\;^\mathrm{o}C\)).

Nosotros consider two types of holes now:

• Hot pigsty: The points sampled from the pigsty boundary are fix to the maximal temperature (\(u = 1\;^\mathrm{o}C\));
• Cold pigsty: Conversely, in this case, the points sampled from the hole boundary are prepare to the minimal temperature (\(u = -i\;^\mathrm{o}C\)).

…Running

Let's now go some code running! The teaching in the control line that leads to the PINN results is the following:

          python heat_idrlnet.py --max_iter=10000 --output_folder=hot_hole --holes_list=0,0,0.i --output_num_x=500 --output_num_y=500 --colorbar_limits=-1.5,1.5                  

For instance, the cold pigsty setting can be run as:

          python heat_idrlnet.py --max_iter=10000 --output_folder=cold_hole --holes_list=0,0,0.1 --holes_temp=-1 --output_num_x=500 --output_num_y=500 --colorbar_limits=-ane.5,1.five                  

Regarding the new flags in these command lines:

• holes_list is the listing of holes we consider in our plate, where each group of iii contiguous entries define a hole every bit \((x_\rm{center}, y_\rm{middle}, radius)\) ;
• holes_temp defines the temperature of the holes boundaries (it is not divers for the hot hole as it is \(1\;^\mathrm{o}C\) by default);

And so, for the same \(u_{\rm top} = i\;^\mathrm{o}C\), we see the divergence in the profile for both the cold and hot hole edge scenarios:

Fig. 5: Estrus diffusion profiles for a hot [top] and cold [bottom] temperature of the hole purlieus. Case on bespeak: small changes in parameters tin result in very dissimilar outputs! Credits: Manuel Madeira / Inductiva

Woah! The results from these experiments are articulate: the pigsty in the domain conspicuously affects the oestrus diffusion profile in very different outputs!

• When the pigsty boundary is cold, the heat source remains the same and and so the same general downward parabolic-like behavior we've discussed is observed. The main difference is that heat flows around the hole.
• The more than interesting case occurs when nosotros also pump energy into the plate through the hole boundary. In that case, some other design is added – a radial outflow. The interference between these ii streams is obtained in contrary directions: while the common cold pigsty suppresses the heat diffusion towards closer regions to the hole border.

Only this is still intuitive enough. Merely how to call back of a highly circuitous interference pattern? Let's put our code handling more than exotic domains!

For instance, let's think of more physically-relevant cases. Can nosotros understand the physics behind this irregular setting where 3 holes of various sizes and positions are found and the boundary is at present curved?

Fig. six: Heat period across a more complex domain composed of three holes of varying sizes and positions, as well as curved left and correct boundaries. Credits: Manuel Madeira / Inductiva

Generalizing through grid-searching (is inefficient)

To make a point (and become more awesome visualizations 😁), let's see how the output changes by changing the diffusitivity rate \(D\) for the hot hole scenario.

For that, we simply run each PDE for each \(D\):

Fig. 7: Heat diffusion profile in the holed domain by ramping up the diffusitivity from \(D=0.01\) [peak] to \(D=0.1\) [eye] and \(D=1\) [bottom]. Notation that each PINN had to be trained individually. Credits: Manuel Madeira / Inductiva

Hot! Nosotros can see that the diffusitivity allows usa to uncrease both phenomena streams we discussed (downward vs radial). Additionally, information technology sets the time scale for equilibration, when the state becomes stationary i.eastward. whenever \(\frac{\partial u}{\partial t} = 0\)

The master betoken to grab here though is that the output yous run into comes later on preparation each PINN individually! For instance, for these settings, each PINN will take near 5 hours. This is completely inefficient and does not allow the algorithm to organically understand how to map the IBCs to the output.

The PINN architecture behind generalization

In order to make generalization tangible, the calculating infrastructure needs to be versatile and efficient. From a computational perspective, we should inquire:

How exactly does the PINN change to accommodate for this generalization?

The fact that the loss function differs according to the domain from where the data domain points considered are sampled is of huge computational relevance.

While a initial or boundary point is straight fit by the PINN to its target (imposed past the initial or boundary condition itself), a point stemming from an interior domain contributes to the fitting procedure through its PDE residue [two].

PINNs exercise non impose an upper limit to the number of IBCs or interior domains. Each of these IBCs may accept a different target and each interior domain might be assigned to dissimilar PDEs. Every bit you tin imagine, for circuitous problems, PINNs accept a high chance of turning into a mess!

Let's make use of a perk from the IDRLnet library (which supported u.s.a. throughout the Heat serial) — a visual representation of the computational graph (in terms of IDRLnet nodes) underneath the implementation it receives.

For this our instance, the representations obtained tin can be visualized as:

Fig. viii: Computational graphs considered by IDRLnet for each sampling domain considered. If we added holes to our plate, an extra graph would be obtained (similar to the ones from the IBCs). Credits: Manuel Madeira / Inductiva

Note that the blue nodes are obtained by sampling the different domains considered (DataNodes), the scarlet nodes are computational (PDENodes or NetNodes), and the dark-green nodes are constraints (targets). [2]

Having a graphical representation of what is going on within our code is ever helpful. Naturally, this tool may become extremely handy to ensure that the problem solution is well implemented.

Our fiery conclusions on Neuro-Solvers

This post completes the Heat serial.

Well, it has been quite a ride! To terminate off the Estrus series, we took the opportunity to sail through seas that classical methods can not achieve (or at to the lowest degree through simple procedures). The reason is that they are not scalable with increasing parameter customization. Classical methods have underwhelming potential in providing dispatch into solving PDEs.

We debate Neural Networks have the capability of streamlining these high-dimensional increments by generalizing more smartly. Just the complication has been transferred to other problems. As nosotros alluded earlier, the option and fine-tuning of variables and parameters is not something trivial to achieve (either through classical and DL frameworks).

To see how versatile NNs tin can exist, we pushed a niggling harder and checked if adding more complication could be coped by Physics-Informed Neural Networks (PINNs). In a modest setup of incremental difficulty, we sure have explored a lot of situations and probed potential means to achieve smarter grooming.

This strategy of adding new parameters equally simple inputs to achieve generalization is the simplest 1 (just arguably not the most efficient i).

There are several alternatives — a bully example is HyperPINNs [i], whose results have been published recently. They event from the fusion of hypernetworks and the more conventional PINNs. Virtually chiefly, HyperPINNs take been shown to succeed in achieving generalization — although in a different implementational flavor.

The outlook message to us is elementary to state. The issues pointed out and run experiments illustrate 2 essential aspects that will demand to proceed being optimized are different in nature:

• the power that Machine/Deep Learning techniques have to propel scientific calculating to unseen new paradigms;
• the challenges in computation and algorithm architecture acquired by evermore realistic and refined systems of interest.

We at Inductiva are precisely learning to empathize how Automobile Learning can be used to expand our noesis of Partial Differential Equations to realms never computed earlier.

Stay tuned by following our new blog posts!

🔥🔥🔥 Fire out 🔥🔥🔥

[ane] A great introduction to HyperPINNs!
[2] More information about the PINN loss and nodes in Oestrus #2.

Credits & Thanks

We thank our Inductiva pals — Manuel Madeira (main author), David Carvalho (editor and co-author), Fábio Cruz (technical editor and reviewer).

From usa at Inductiva, it has been a hot ride.

fordhoughte1983.blogspot.com

Source: https://inductiva.ai/blog/article/heat-3-neurosolver

Share this post